https://www.cnblogs.com/idorax/p/6441043.html

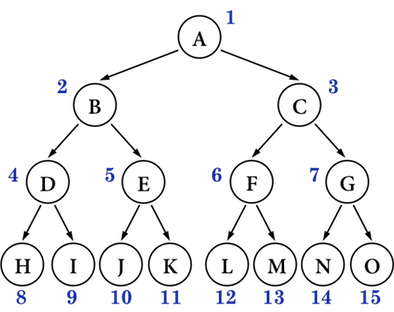
(1) 一棵完美(Perfect)二叉树看起来是这个样儿的， 【图2.6.1】

（2） 那么，将编号为15, 14, ..., 9的叶子结点从右到左依次拿掉或者拿掉部分，则是一棵完全(Complete)二叉树,

例如，将上图中的编号为15, 14, 13, 12, 11叶子结点都拿掉(从右到左的顺序)， 【图2.6.2】

image.png

（3） 下图就不是一棵完全(Complete)二叉树，【图2.6.3】，

如果将编号11(K)结点从编号6(E)的左儿子位置移动到编号5(E)的右儿子位置，则变成一棵完全(Complete)二叉树。

image.png

注： 图2.6.1， 2.6.2和2.6.3均来自：http://alrightchiu.github.io/SecondRound/binary-tree-introjian-jie.html， 但是，其将Full Binary Tree当做就是Perfect Binary Tree, 我认为是不正确的，特此说明。

特别说明： 其实，理解完全(Complete)二叉树可以借助于**栈(stack)**的思想。 例如，把图2.6.1中的完美(Perfect)二叉树的所有结点按照编号1, 2, 3, ..., 15依次入栈(push)。 那么，对栈的每一次出栈(pop)操作后，栈里保存的结点集对应到图2.6.1上去都是一棵完全(Complete)二叉树。